Using Art to Teach Computation and Geometry in Tanzania

Working on the Global Learning XPrize was an incredible experience. I love the vision that any child should have access to a world-class education. But to me, having a world-class education is more than just learning to read, write, and do math. A world-class education is not just formal learning, but having world-class toys to play with. I had a fortunate upbringing where I had toys like Lego and K’Nex to build things, computer and video games to explore new worlds, and origami and other crafts to further express my creativity.

I was impressed by Team KitKit, one of the co-grand-winners of the Global Learning XPrize, and their commitment to this mission of giving kids world-class toys to play with. At the Global Learning Summit in May, team KitKit shared some photos of drawings that the kids had made using their drawing tool. This was by far my favorite part. Not just reading, writing, and math, but also a place for kids to explore their creativity. They used the tool to practice their number and letter-drawing skills. They used the tool to draw things around them like flowers, houses, and cars.

What the children drew

What’s wonderful about the Global Learning XPrize is that all of the teams’ code has been open-sourced, so anybody can experiment with the source code. There are some ideas around art, math, and computation that I have been wanting to explore for a long time, so KitKit’s drawing app is a perfect opportunity to do so.

Computers are Different than Paper

The KitKit creative suite contains many toys like the drawing pad, a marimba, and a drum. It’s great that they’re giving these kids tools to play with, but I think that we can go even bigger and better. The drawing app is a big blank piece of paper, with a selection of brightly colored crayons to choose from on the side. While making this tool into an app provides valuable functions that the analog world doesn’t provide (like saving drawings without taking up physical space), the tool is effectively the same as what would be available on an analog piece of paper. The idea that the digital world should reflect digital capabilities, and not just analog capabilities, is something I’ve learned from reading a lot of work by computer scientist and designer, Bret Victor.

We have these things called computers, and we’re basically just using them as really fast paper emulators… Now we’re staring at computer screens and moving our hands on a keyboard, but it’s basically the same thing. We’re computer users thinking paper thoughts.

Many of the tools that we have created on the computer are just reproductions of the analog space. A word processor is just a fancy typewriter. To go to the next level of tool evolution, we can enhance our tools to fully utilize the flexibility and power of our computers.

So I’ve been asking myself, is this drawing app just a really fast paper emulator? When a child uses this tool to draw a house or a car or a plant, are they thinking computer thoughts, or are they thinking paper thoughts? More importantly, how can we design and build interfaces that help children to think computer thoughts?

Geometry: Drawing with Radial Symmetry

The first feature I’ve added to KitKit’s Drawing app is a way to draw shapes with Radial symmetry. It’s easy enough to set it so that the same line is repeated at constant intervals.

What it looks like to create drawings with radial symmetry.

Radial symmetry is a great first feature to add… We see radial symmetry in flowers and plants, in the sun, in artwork. And it’s easy to enough to just draw the same line that the finger is drawing, but shifted at consistent angles.

Photos go here

There are lots of possibilities (see photos). I’d like to put this tool in front of children and see what they do with it!

Computation: Repetition and Symbols

The second feature I’ve added is the ability to create multiple similar drawings in parallel. The user “plant seeds” and then draws once, while the computer repeats their drawing from each of the seeds they planted. This can be used to do things like build identical houses or grow identical crops. I like the metaphor of “planting a seed” and then growing a crop from that seed because it uses a metaphor that many students in rural areas are familiar with. In the village which our team did our research, over half of the students’ parents worked as farmers. The repetitive nature of planting seeds and nurturing those seeds is a metaphor that lends itself similar to computation.

Photos go here

By storing the seeds’ angles along with their positions, we can give the user the ability to grow seeds in any direction. This allows for many more forms of creativity, such as leaves on a tree, or more complex repetitive patterns.

gif goes here

photos go here

We can even combine the radial tool with the vector parallel tool to create things like flowers on branches! By giving kids multiple tools that are implemented using mathematical and computational methods, we can expand their imagination for what is possible to draw.

photo goes here

Connecting to Culture

At a tech conference in Dar Es Salaam, I met a South African artist named Ralph Borland. He adds electronic parts to South African wire art to make African Robots that can move or react to touch and light. I loved that he added to an existing local art form to add a new element to it. I believe that we can do something similar and connect computational and geometric principles to Tanzanian or African art. I found a possible answer to this question at a place in Dar Es Salaam called the Tinga Tinga Arts Collective. They make hundreds of paintings in this art style, much of which is sold to tourists. And upon further research, the art style may have roots in traditional East African art. Admiring the paintings, I couldn’t help but notice the repetition and geometry in many of them. Notice the two paintings below of fish with their radial spirals, just the kind of pattern that computers are great for making. Perhaps we can make a connection to the field of Ethnomathematics. These artists are already doing their paintings in a way similar to how a computer might, so the connection is right there!

Tinga Tinga photos

I loved seeing this style of painting. The painters could draw the same animal or pattern over and over again, and the whole would be more than the sum of its parts. Let’s dive into one specific painting and find principles of computation and geometry hidden within.

Here’s one of the paintings I purchased. There are a few common elements we can see repeated throughout:

• The purple birds.
• The red circular flowers.
• The tiny green dots representing leaves.
• The concentric oval patterns on the tail of the bird on the right.

A Tingatinga painting with lots of repetition.

This took a lot of skill to paint, and the artist gets a lot of mileage from painting the same pattern in different configurations. Could we use a piece of artwork like this as an example to help learners think computationally? Can we help them see this as a collection of repeated patterns, i.e. something that could be facilitated with a computer?

We can break it down into layers. Each head is the same pattern in a different (x,y) location. Each neck is a purple shape stretched along a series of points. Each flower is the same pattern in a different (x,y) location.

How a painting could be broken down into computation-friendly layers.

What I like about these paintings is that they can provide a vision for how a drawing tool could be used to create computationally complex artwork. Imagine giving learners the tools to create complex artwork like this, and then letting them change the whole painting by altering one little variable instead of repainting every little detail. For example, what will the painting look like if you change the color of the flowers?

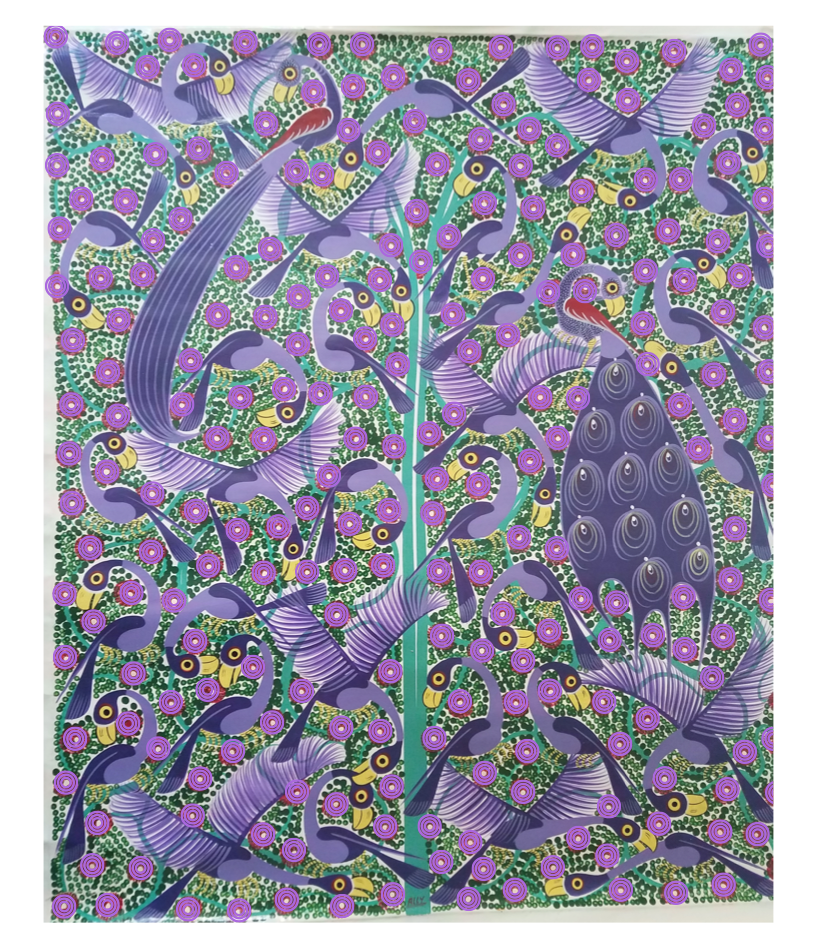
what would it look like if we changed the color of the flowers?

Designing a good system

Even if we can (a) implement cool drawing features and (b) provide a vision for the types of drawings that can be made, we must still address this issue posed here by Bret Victor.

a well-designed system is not simply a bag of features. A good system is designed to encourage particular ways of thinking, with all features carefully and cohesively designed around that purpose.

We can’t just give students a fancy drawing tool with all these neat features and expect them to learn math or “computational thinking”. How can we build the user experience so that they are actually thinking in the ways we want them to? And can we better define those ways of thinking? The system must be built with good principles of interaction design and learning science.

Moving Forward

Here are some of my next steps for working on this project:

• User testing: I would like to polish the existing features by running user tests with both adults and children. Testing with adults will help me get new eyes on it for suggestions, and testing with children will test whether it’s usable and understandable by the target age group.

• More features: There are so many possibilities for how computer programming and geometry can intersect with drawing. I will continue to ideate new possible features, then develop them.

• The marimba and drum apps: As I mentioned briefly above, KitKit has apps for playing the marimba and an African drum. I’ve already made some changes to the marimba app, and I will continue to experiment!

Experiment with the code

See the original code here

And my changes here